Gradient Boosting
Unlike Random Forest, which constructs independent trees on bootstrap samples to reduce variance and improve generalization, Gradient Boosting builds trees sequentially, where each new tree aims to correct the errors made by the previous ones to achieve higher predictive accuracy.
Gradient Boosting enhances the final prediction function, \(F(x)\), by combining \(M\) \textbf{weak learners}. In this approach, each subsequent weak learner is trained to minimize the residual errors (mistakes) of the preceding learners, and the aggregation of all weak learners produces a strong predictive model. Assuming \(f_{i}(x)\) represents the \(i\)-th weak learner, the overall model is expressed as [2]
\[ F(x) = \sum_{i=1}^{M} f_{i}(x) \]
To implement this, the algorithm first initializes a loss function and an initial weak learner. The loss function must be differentiable, as Gradient Boosting is a gradient-based optimization procedure. The algorithm begins with an extremely weak learner, \(f_{1}(x)\) [2].
For each learner \(f_{j}(x)\), where \(j = 1, \ldots, M\), the algorithm computes the negative gradient of the loss function w.r.t. the predictions, i.e., [2]
\[ \hat{r}_{ji} = - \frac{\partial \mathcal{L}(y_{i}, \hat{y}_{i})}{\partial \hat{y}_{i}} \bigg|_{\hat{y}_{i} = F_{j}(x_{i})}, \]
where \(y_{i}\) and \(\hat{y}_{i}\) are the actual and predicted values corresponding to the input \(x_{i}\), respectively [2].
Next, the new weak learner, \(f_{j+1}(x)\), is trained on the residuals \(\hat{r}_{j}\) (i.e., the computed gradients) along with the original input data \(X\). The contribution of this new weak learner, denoted as \(\hat{\gamma}_{j+1}\), is obtained by solving [2]
\[ \hat{\gamma}_{j + 1} = \argmin_{\gamma} \sum_{i=1}^{N} \mathcal{L} \left( y_{i}, F_{j}(x_{i}) + \gamma f_{j+1}(x_{i}) \right) \]
The model is then updated as [2]
\[ F_{j + 1}(x) = F_{j}(x) + \hat{\gamma}_{j + 1} f_{j + 1}(x) \]
This process continues iteratively until the algorithm converges to the optimal solution (i.e., the minimum loss) [2].
Comparison with Random Forest:
-
Since each weak learner in Gradient Boosting is trained to correct the errors of its predecessors, it often achieves higher predictive accuracy than Random Forest.
-
However, Gradient Boosting is slower to train and more complex to tune, as it involves more hyperparameters.
-
It is also more susceptible to overfitting if not properly regularized (e.g., via learning rate, subsampling, or tree depth constraints).
Implementation
The machine learning random fores model in Python was developed from scratch. The complete implementation script is available on Gradient Boosting from Scratch.
Classifier
We developed a gradient boosting classifier for the Breast Cancer dataset using the built-in functions provided in scikit-learn [1] in Python. The following screenshot illustrates the training process of the classifier. The model was imported from sklearn.ensemble. Moreover, we applied Grid Search Cross-Validation to identify the optimal hyperparameters of the model. In this process, we defined ranges for various various parameters, such as n_estimators (no. of trees), max_depth, min_samples_split, and learning_rate.
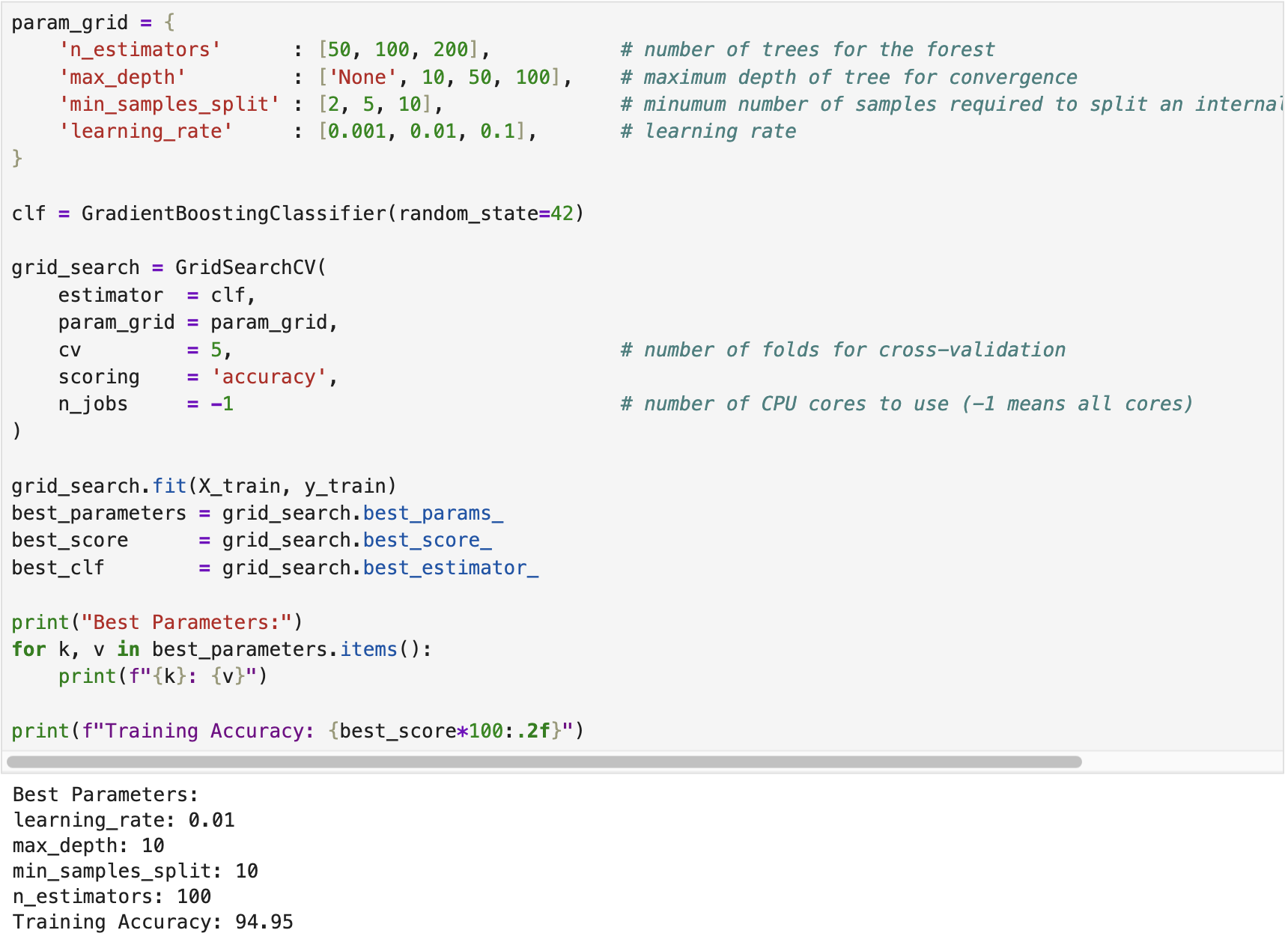
After identifying the best classifier through Grid Search Cross-Validation, we evaluated its performance using the test dataset. The following screenshot presents the corresponding results. The complete implementation script is available on the GitHub page Gradient Boosting Classifier.

Regressor
We developed a gradient boosting regressor using the California Housing dataset available in scikit-learn. The following screenshot shows the training (fitting) process of the regressor, where Grid Search Cross-Validation was employed to tune the optimal hyperparameters.
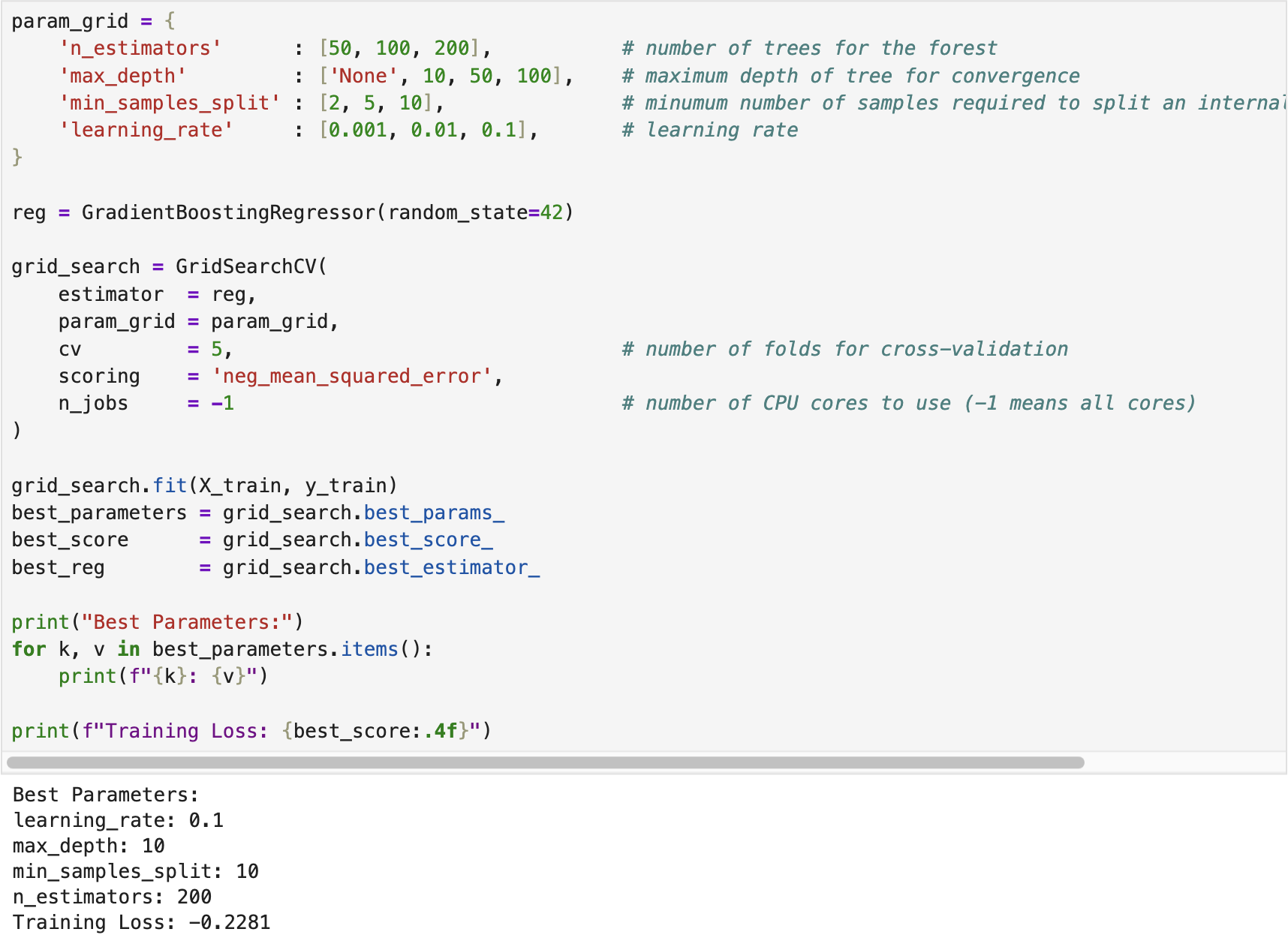
After training the regressor, we evaluated its performance on the test dataset. The following screenshot displays the corresponding results. The complete implementation script is available on the GitHub page Gradient Boosting Regressor.

XGBoost
Extreme Gradient Boosting (XGBoost) is an enhanced variation of the traditional Gradient Boosting algorithm that provides significant improvements in speed, accuracy, and feature handling. These enhancements are achieved through advanced techniques such as regularization, parallel processing, and a more sophisticated loss function optimization using the second-order Taylor approximation instead of standard first-order gradient descent. Key characteristics of XGBoost include:
-
XGBoost incorporates both L1-norm and L2-norm regularization techniques to prevent overfitting and improve model generalization.
-
It includes built-in mechanisms for handling missing values efficiently, eliminating the need for external preprocessing.
-
XGBoost inherently supports cross-validation, which helps in reducing overfitting and improving model robustness.
-
It is computationally efficient and supports parallel processing via leveraging multi-core architectures for faster training and tuning.
-
XGBoost employs a depth-first tree growth strategy and stops branching when further splits provide no performance gain. The model then performs backward pruning to optimize the final tree structure.
-
It supports user-defined objective functions and evaluation metrics that enhances versatility and provides flexibility for a wide range of learning tasks.
Compared to traditional Gradient Boosting, XGBoost leverages a Taylor series approximation of the loss function to accelerate convergence. In XGBoost, the overall objective function is defined as
\[ \mathcal{L}(\Phi) = \sum_{i}\mathcal{L}(y_{i}, \hat{y}_{i}) + \sum_{k}\Omega(f_{k}), \]
where the first term represents the residual loss w.r.t. the samples, aiming to minimize the bias, and the second term denotes the regularization component over all trees, aiming to control model complexity and reduce variance.
The residual loss at iteration $t$ combines the predictions of all previous trees with the contribution from the current tree, such that
\[ \mathcal{L}(y_{i}, \hat{y}_{i}) = \mathcal{L}(y_{i}, \hat{y}_{i(t-1)} + f_{t}(x_{i})), \]
where \(\hat{y}_{i(t-1)}\) represents the aggregated predictions from the previous \((t-1)\) trees, and \(f_{t}(x_{i})\) corresponds to the prediction of the current tree.
To efficiently optimize this objective, XGBoost applies a second-order Taylor series approximation to the loss function around \(\hat{y}_{i(t-1)}\), that yields in
\[ \mathcal{L}(y_{i}, \hat{y}_{i(t-1)} + f_{t}(x_{i})) \approx \mathcal{L}(y_{i}, \hat{y}_{i}) + g_{i}f_{t}(x_{i}) + \frac{1}{2}h_{i}f_{t}^{2}(x_{i}), \]
where \(g_{i}\) and \(h_{i}\) denote the first- and second-order derivatives (gradient and Hessian) of the loss function w.r.t. the previous prediction, defined as \(g_{i} = \partial_{\hat{y}_{i(t-1)}}\mathcal{L}(y_{i}, \hat{y}_{i(t-1)})\) and \)h_{i} = \partial^{2}_{\hat{y}_{i(t-1)}}\mathcal{L}(y_{i}, \hat{y}_{i(t-1)})\).
Classifier
We developed an XGBoost classifier for the Breast Cancer dataset using the built-in functions provided in scikit-learn [1] in Python. The following screenshot illustrates the training process of the classifier. The model was imported from xgboost. Moreover, we applied Grid Search Cross-Validation to identify the optimal hyperparameters of the model. In this process, we defined ranges for various various parameters, such as n_estimators (no. of trees), max_depth, min_samples_split, and learning_rate.

After identifying the best classifier through Grid Search Cross-Validation, we evaluated its performance using the test dataset. The following screenshot presents the corresponding results. The complete implementation script is available on the GitHub page XGBoost Classifier.

Regressor
We developed an XGBoost regressor using the California Housing dataset available in scikit-learn. The following screenshot shows the training (fitting) process of the regressor, where Grid Search Cross-Validation was employed to tune the optimal hyperparameters.
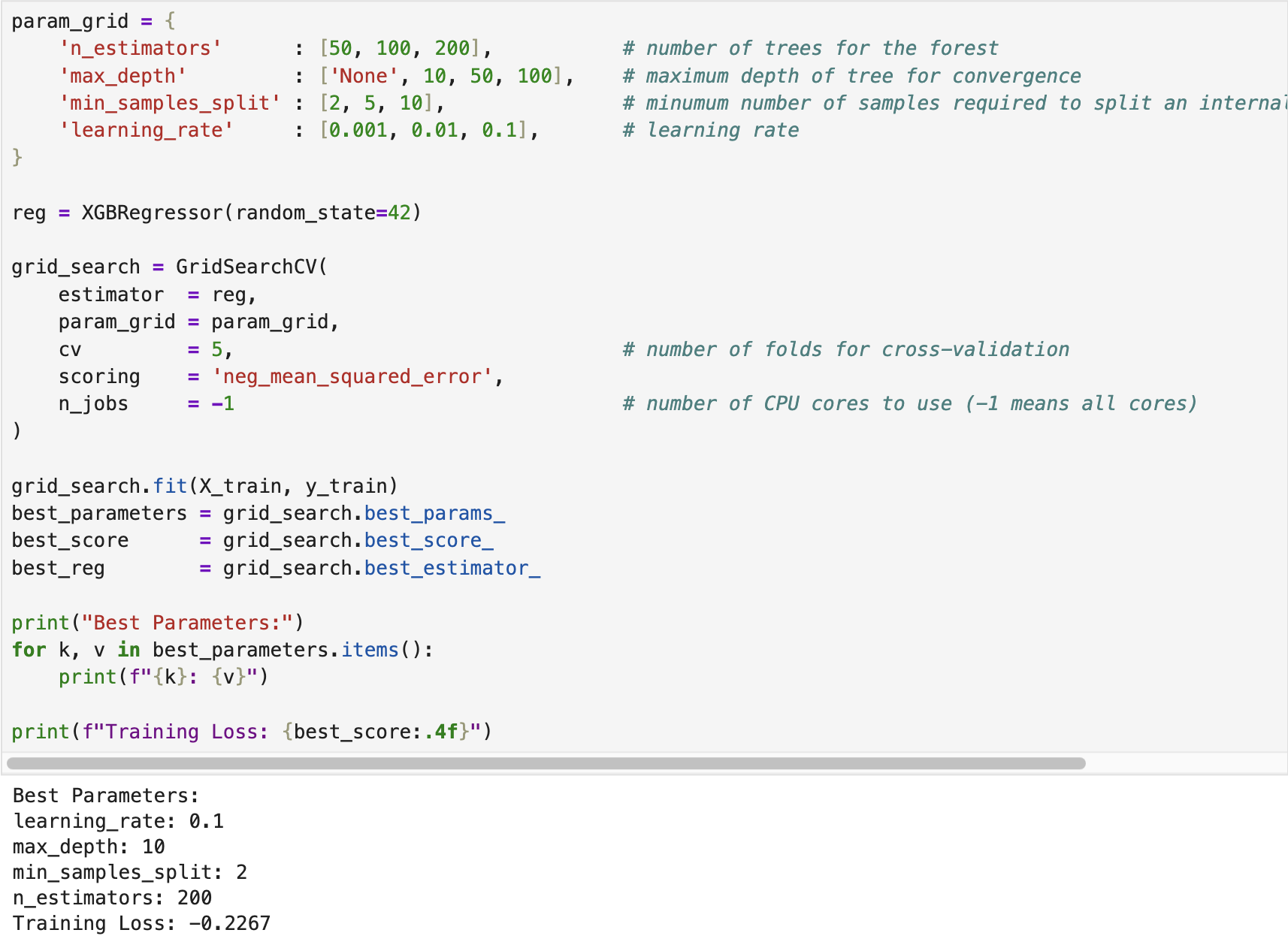
After training the regressor, we evaluated its performance on the test dataset. The following screenshot displays the corresponding results. The complete implementation script is available on the GitHub page XGBoost Regressor.

References
[1] F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay, “Scikit-learn: Machine learning in Python,” Journal of Machine Learning Research, vol. 12, pp. 2825–2830, 2011.
[2] ritvikmath, “Gradient Boosting : Data Science's Silver Bullet,” ritvikmath, accessed: September 29, 2021, https://www.youtube.com/watch?v=en2bmeB4QUo&t=608s.

 IEEE
IEEE Web of Science
Web of Science