Decision Tree
A decision tree is an algorithm that recursively splits a dataset into subsets based on its features. The splitting criterion is typically determined using one of two metrics, i.e., Information Gain (IG) or Gini Index.
-
Information Gain: IG is based on entropy, which quantifies the level of uncertainty or randomness in the information being processed. IG measures the reduction in entropy that results from partitioning the dataset according to a given feature. To calculate the IG, we have
\[ \text{IG(D, A)} = \text{H(D)} - \text{H(D|A)}, \]
where D and A are the dataset and the feature, respectively; H(D) represents the entropy of the dataset; and H(D|A) shows the entropy of the dataset w.r.t. the feature A (conditional entropy). The entropy of a set S, where \(\{\text{A, D}\in\text{S}\}\) is given by
\[ \text{H(S)} = -\sum_{x\in S}p_{i}(x)\log(p_{i}(x)), \]
where \(p_{i}\) is proportion of the \(i\)-th class in the set.
-
Gini Index: Gini Index measures the probability that a randomly chosen instance would be misclassified if it were labeled according to the class distribution in the dataset. Therefore, we have
\[ \text{H(S)} = 1 -\sum_{x\in S}p^{2}_{i}(x), \]
where \(p_{i}\) is the probability of an instance belonging to class \(i\).
Overall, an IG–based model aims to maximize IG, while a Gini Index–based model aims to minimize the Gini value. IG is generally more suitable for imbalanced datasets, whereas the Gini Index is computationally simpler to implement.
Numerical Example
Given the data in Table 1, we perform the decision tree algorithm based on IG.
| Neighborhood | No. of Rooms | Affordable |
|---|---|---|
| West | 3 | Yes |
| West | 5 | Yes |
| West | 2 | Yes |
| East | 3 | Yes |
| East | 4 | Yes |
| East | 6 | No |
| East | 5 | No |
| East | 2 | Yes |
First, we calculate the entropy of the data w.r.t. the labels (i.e.,
"Affordable" feature). Considering 6 data points labeled as "Yes" and
2 data points labeled as "No" (see Fig. 1), the probabilities of "Yes"
(\(p_{yes}\)) and "No" (\(p_{no}\)) are equal to \(p_{yes} = 6/8\) and
\(p_{no} = 2/8\). Therefore, we have
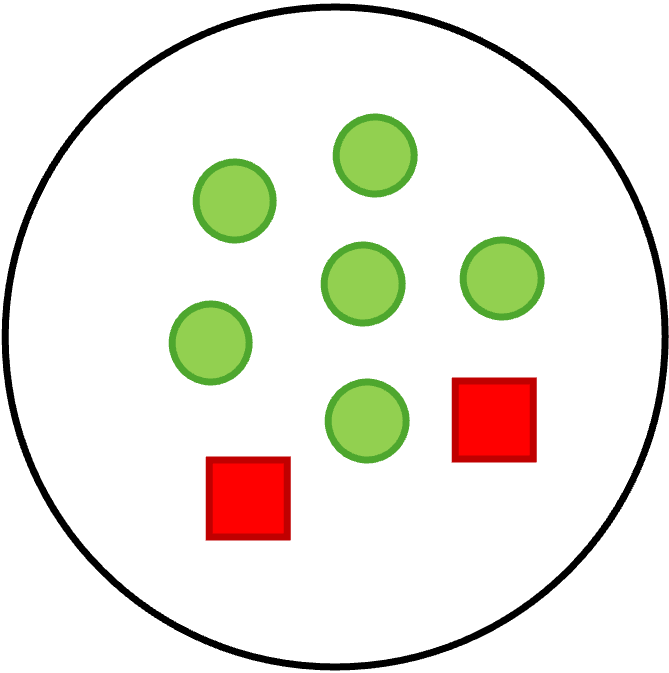
\[ \begin{split} \text{H(D)} =~& -p(Y=yes)\log(p(Y=yes)) -\\ & ~~~p(Y=no)\log(p(Y=no))\\ =~& -\frac{6}{8}\log(\frac{6}{8}) - \frac{2}{8}\log(\frac{2}{8}) = 0.81 \end{split} \]
In the next step, the data samples must be split based on the features, i.e., "Neighborhood" and "No. of Rooms", separately. The corresponding IG needs to be calculated for each feature, and the feature with the highest IG is chosen as the splitting feature. Thus, we have
\[ \begin{split} \text{H(D|Neighborhood)} =~& \text{H(D|Neighborhood=West)} + \text{H(D|Neighborhood=East)}\\ =~&\text{H(Y=yes|Neighborhood=West) + H(Y=no|Neighborhood=West)} +\\ & \text{H(Y=yes|Neighborhood=East) + H(Y=no|Neighborhood=East)}\\ =~&-\frac{3}{8}\left(\frac{3}{3}\log(1) + \frac{0}{3}\log(0)\right) - \frac{5}{8}\left(\frac{3}{5}\log(\frac{3}{5}) + \frac{2}{5}\log(\frac{2}{5})\right) = 0.61 \end{split} \]
\[ \begin{split} \text{H(D|No. of Rooms)} =~& \text{H(D|No. of Rooms<5)} + \text{H(D|No. of Rooms}\geq 5)\\ =~&\text{H(Y=yes|No. of Rooms<5) + H(Y=no|No. of Rooms<5)} +\\ & \text{H(Y=yes|No. of Rooms}\geq 5) + \text{H(Y=no|No. of Rooms}\geq 5)\\ =~&-\frac{5}{8}\left(\frac{5}{5}\log(1) + \frac{0}{5}\log(0)\right) - \frac{3}{8}\left(\frac{1}{2}\log(\frac{1}{2}) + \frac{2}{3}\log(\frac{2}{3})\right) = 0.35 \end{split} \]
Therefore, IG for each group is calculated as
\[ \begin{split} & \text{IG(D|Neighborhood)} = 0.81 - 0.61 = 0.2\\ & \text{IG(D|No. of Rooms)} = 0.81 - 0.35 = 0.46 \end{split} \]
Since \(\text{IG(D|No. of Rooms)} > \text{IG(D|Neighborhood)}\),
we choose "No. of Rooms" as the splitting feature.
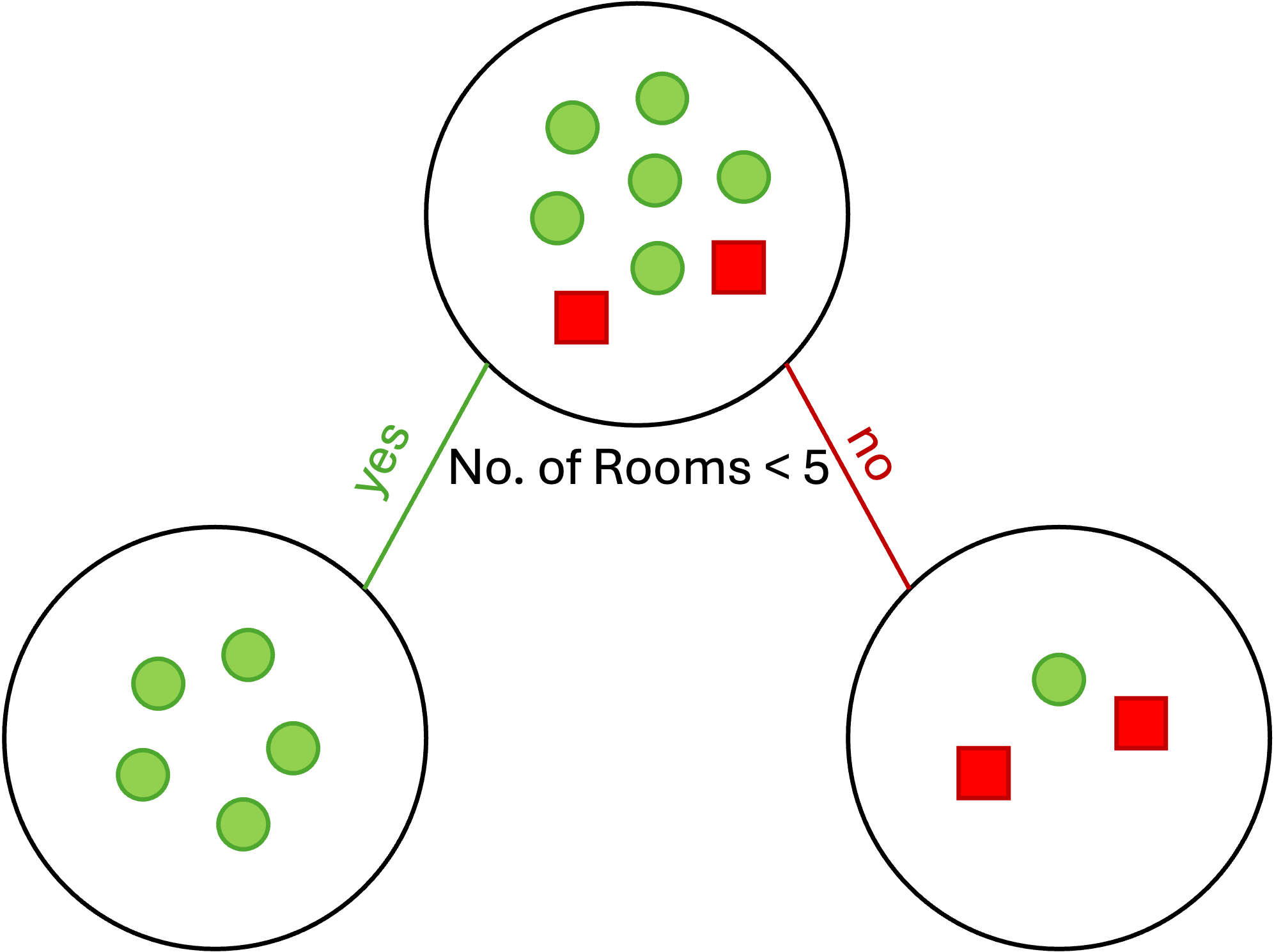
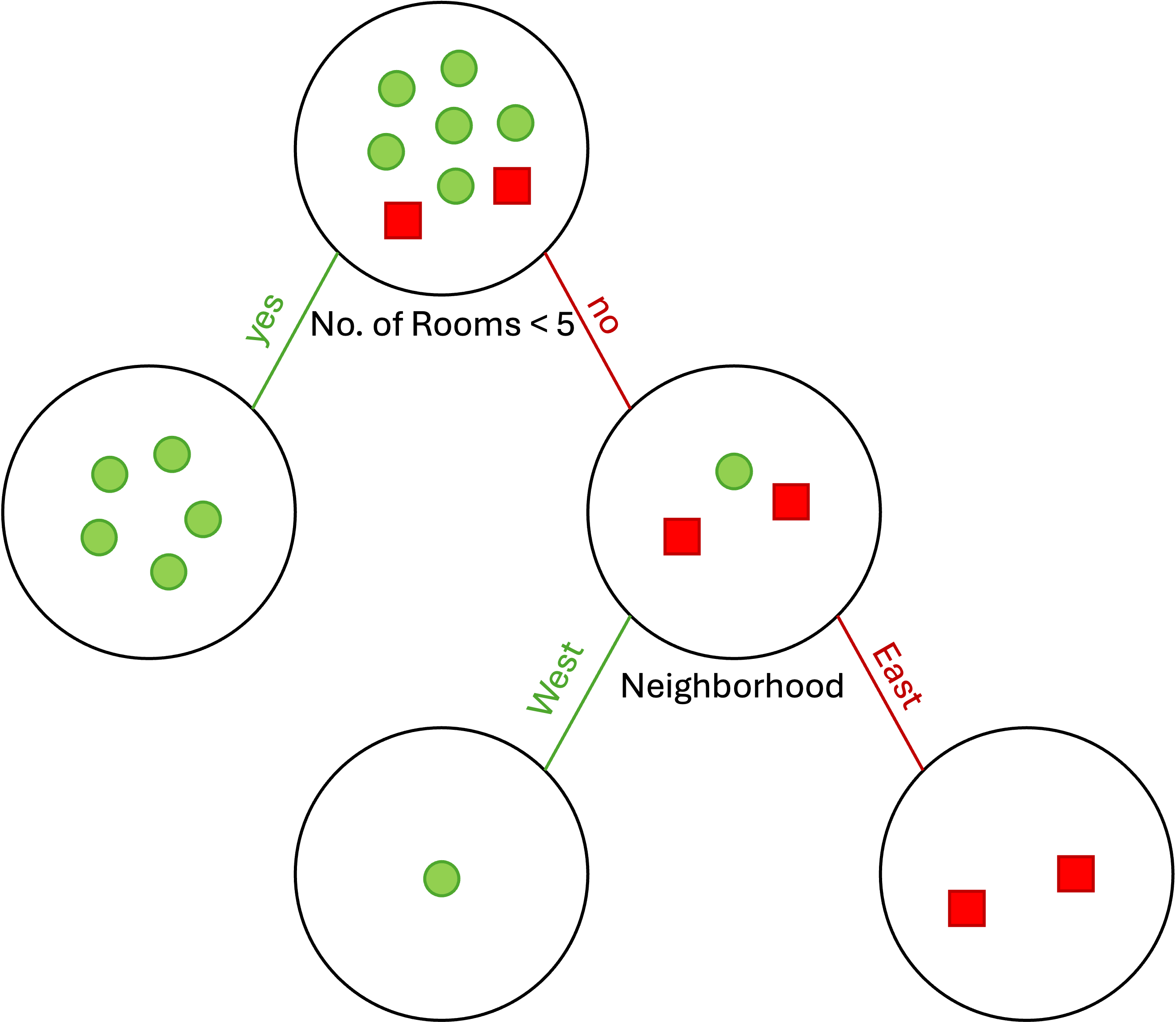
In the next round, since the entropy of the left child of the tree is zero
(all samples belong to the same class, i.e., "Yes"), we split the right
child of the tree w.r.t. the "Neighborhood". Therefore, we have
Implementation
The machine learning decision tree model in Python was developed from scratch following the guidelines provided in [2]. The complete implementation script is available on Decision Tree from Scratch.
Classifier
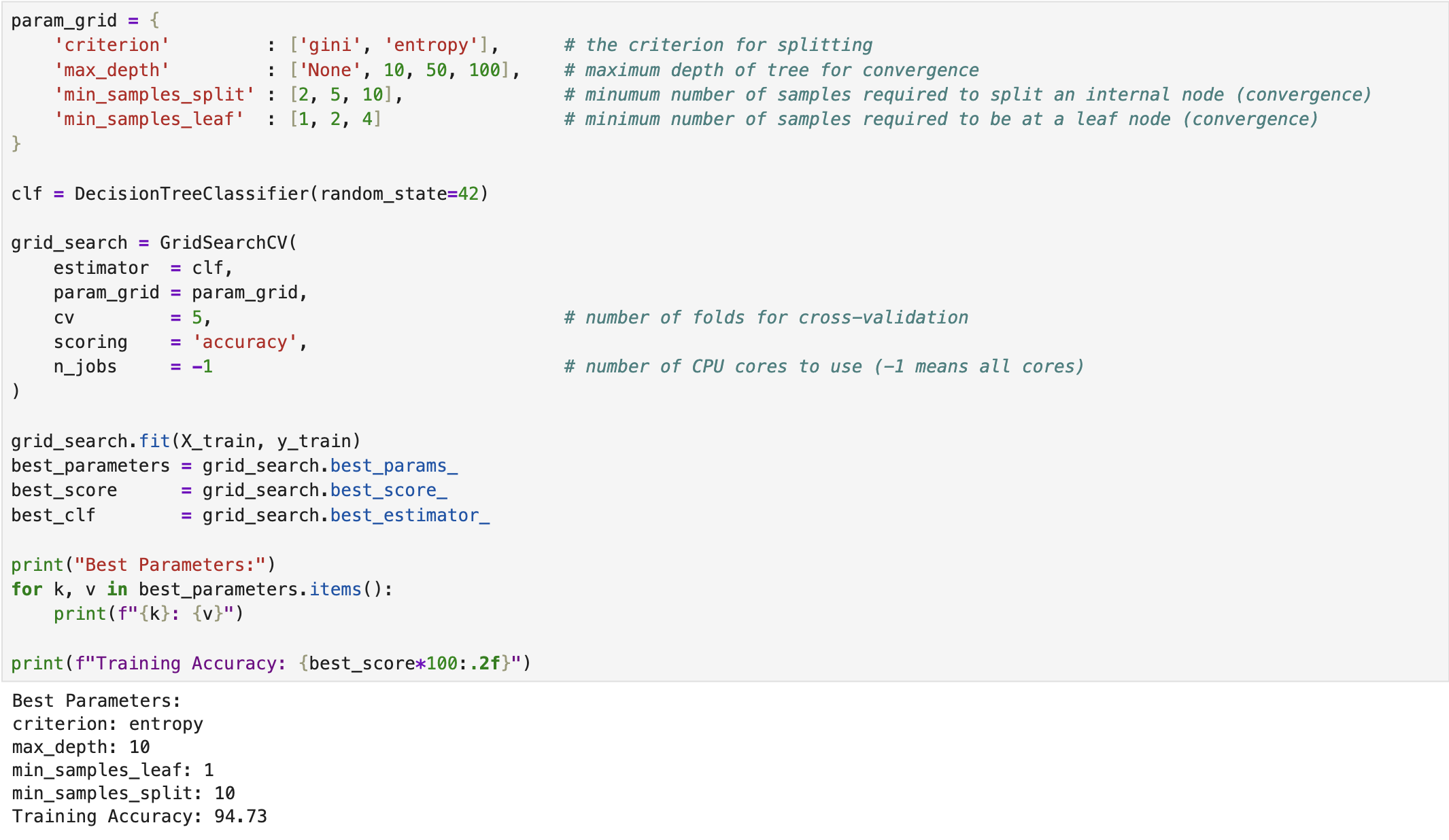
We developed a decision tree classifier for the Breast Cancer dataset using the built-in functions provided in scikit-learn [1] in Python. The following screenshot illustrates the training process of the classifier. The model was imported from sklearn.tree. Moreover, we applied Grid Search Cross-Validation to identify the optimal hyperparameters of the model. In this process, we defined ranges for various convergence criteria, such as max_depth, min_samples_split, min_samples_leaf, and the splitting criterion (i.e., Gini Index or Information Gain).
After identifying the best classifier through Grid Search Cross-Validation, we evaluated its performance using the test dataset. The following screenshot presents the corresponding results. The complete implementation script is available on the GitHub page Decision Tree Classifier.

Regressor
We developed a decision tree regressor using the California Housing dataset available in scikit-learn. The following screenshot shows the training (fitting) process of the regressor, where Grid Search Cross-Validation was employed to tune the optimal hyperparameters.
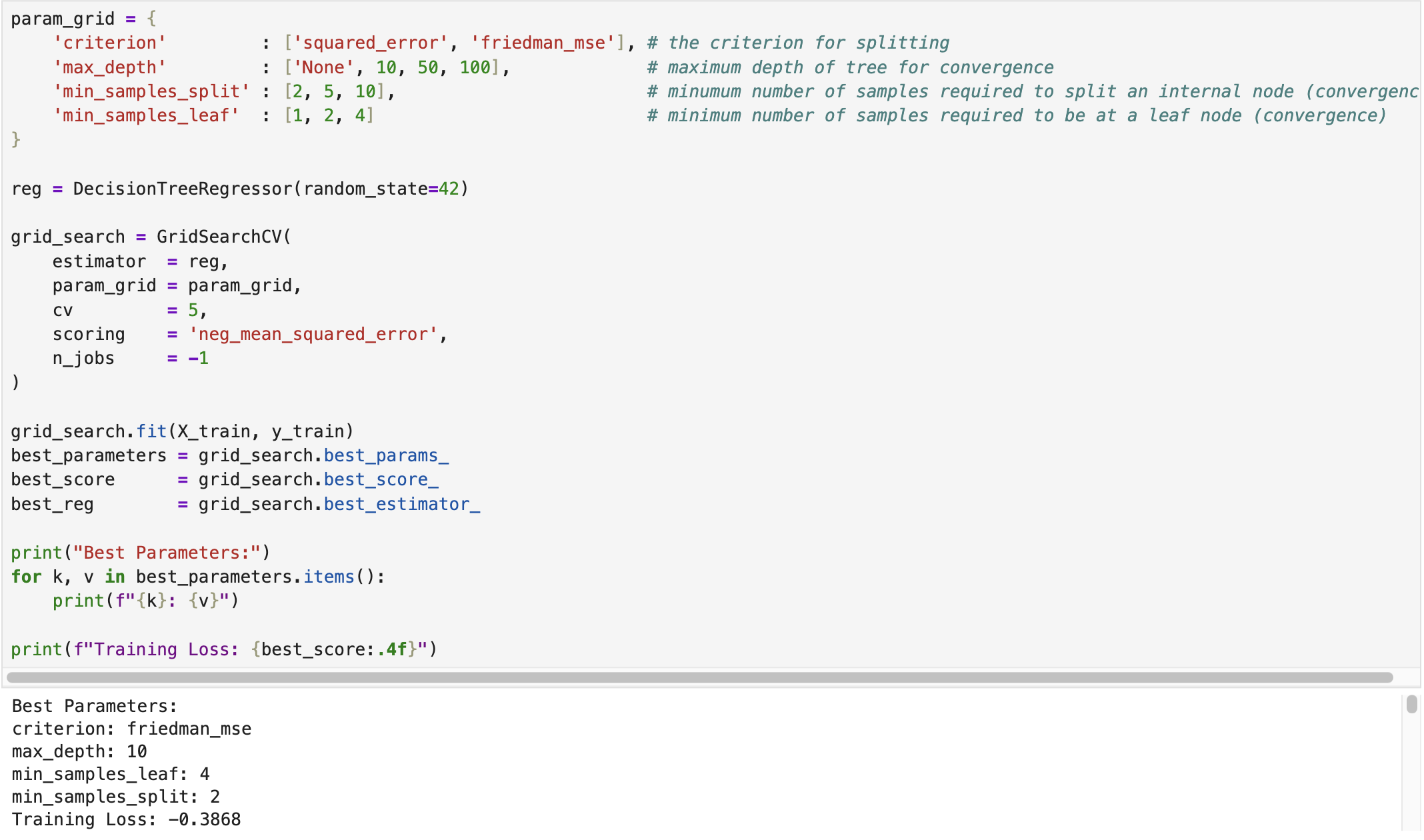
After training the regressor, we evaluated its performance on the test dataset. The following screenshot displays the corresponding results. The complete implementation script is available on the GitHub page Decision Tree Regressor.

References
[1] F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay, “Scikit-learn: Machine learning in Python,” Journal of Machine Learning Research, vol. 12, pp. 2825–2830, 2011.
[2] Misra Turp, “How to implement decision tree from scratch with python,” AssemblyAI, accessed: September 15, 2022, https://www.youtube.com/watch?v=NxEHSAfFlK8.

 IEEE
IEEE Web of Science
Web of Science