Looping Graph

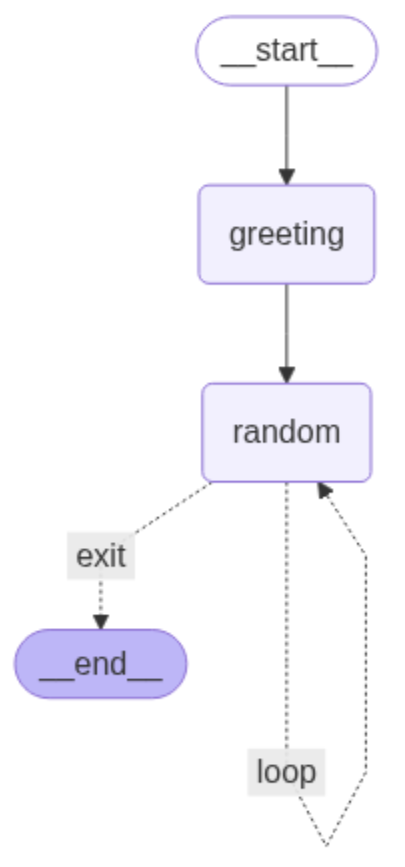
Some graphs are designed to implement looping logic, where data is routed back to previously visited nodes. In such graphs, a cyclic edge is defined for specific nodes, enabling them to transition back to themselves. Figure 1 illustrates the overall flow of a looping graph in LangGraph, which consists of a start state, two nodes (greeting and random), and an end state. The start state is connected to the greeting node via a directed edge (transition). The random node, in turn, has two conditional edges: one that carries the looping condition and routes the flow back to the node itself, and another that connects the random node to the end state [1].

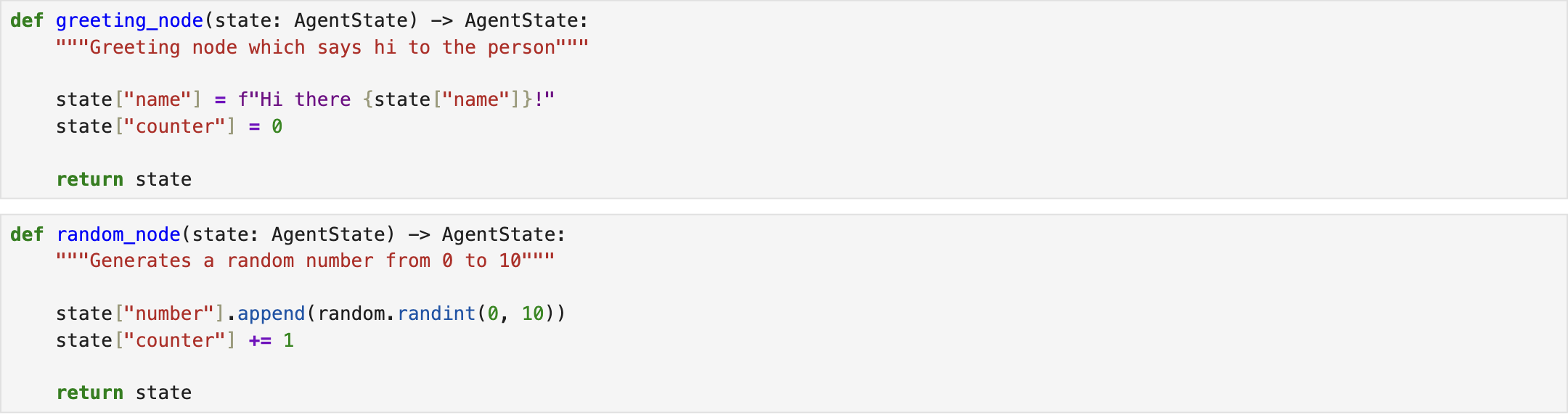
In this example, the system receives the user's first name as input and generates random numbers for specific rounds (e.g., five times here). Finally, the system outputs the message ``Hi there {user’s first name}". In this regard, we first need to create a shared data structure to keep track of information as the application runs. The defined structure, AgentState, records the system's state [1].

Then, the greeting node is defined as a function that receives the user's first name as input and incorporates it into the state information stored in AgentState. The function then returns the updated state. Also, the random node is created to generate random numbers and save them into the state [1].

Moreover, a function is defined to determine whether the system has reached the end state or should continue by entering the loop. The decision is based on a predefined maximum number of iterations required for the process [1].

The next step involves constructing the graph. To begin, we initialize an empty graph in LangGraph, specifying its input type as state (AgentState). We then add the greeting and random nodes to the graph. The greeting node is connected to the start state and random state using deterministic edges. The random node, in turn, includes two conditional edges: one that carries the looping condition and routes the flow back to itself, and another that connects the random node to the end state. Finally, we compile the graph and store it in a variable for subsequent execution [1].

Lastly, we invoke the compiled graph by passing an example first name to that. The results indicate that the designed graph-based system could successfully meet the intended objective [1]. The complete implementation script is available on Looping Graph.

References

[1] freeCodeCamp.org, https://youtu.be/jGg_1h0qzaM?si=69DsFmR2TMN259HC.